Бесплатный O(1) доступ к RAM
Теоретическая информатика — супер крутая вещь. Крайне приятно читать очередной пейпер, рассказывающий про какой-то крутой алгоритм. А, что ещё также приятно — так это Симбиоз Computer science с Реальностью, в которой существует масса ограничений и подводных каммей, на которых принято закрывать глаза в CS.
Сегодня мне попалась на глаза одна прекрасная серия статьей (состоящая из 4 штук) — The Myth of RAM. В этом докладе автор раскрывает глаза на стоимость доступа к памяти. Наверное, это супер очевидная вещь, что O(1) доступ — это несколько преукращенная сущность, и в реальности всё не так. Ведь есть Кэши, Кэш Миссы, Свопы, Сетевое взаимодействие, и масса всего, о чём обычно принято забывать в базовой CS, где мы описываем доступ к случайному элементу в памяти за O(1).
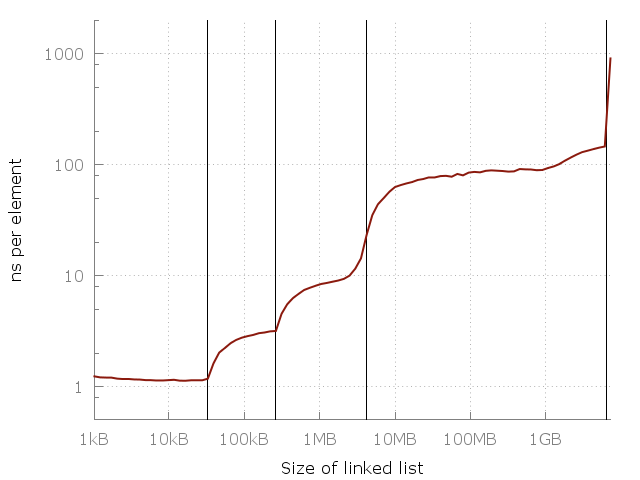
Небольшая выкладка из статьи. Например, рассмотрим стандартный связный список (linked list), состоящий из нод. В каждой ноде есть указатель на следующую, а также некоторый payload. Пусть Связный список состоит из N элементов. Пусть эти N нод требуют для хранения M памяти. Тогда look-up будет стоить не превычные O(N), а O(N sqrt(M)). В случае, если все элементы структуры выравнены в памяти, и занимают одинаковое её количество, тогда M можно оценить, как O(N). В этом случае поиск элемента будет стоит O(N sqrt(N)).
Тут важно понять одну вещь. В нотацию «Большой Оу» (O(N), например), скрытая любая константа, и, это позволяет говорить про чесный O(1) доступ к памяти. Однако, как только дело доходит до практики, и нам дейсвительно надо знать, как будет вести себя алгоритм на больших массивах данных, нужно помнить этот факт про RAM. Это очень отчётливо видно в Теоретической информатике Баз Данных, где все доступы к консистентному хранилищу вполне себе описываются в алгоритмах, потому, что для БД — это супер важно.
Категории: Программирование